Interpret Scan Results for Data Scientists
This page provides an illustrative example of how data scientists interpret scan results from a notebook.
Purpose
In this document, we will use models built on a simple simulated dataset to show how to interpret the different scores Certifai calculates (i.e., robustness, fairness, and performance scores) .
Reference
The figures in this document are generated in Interpreting Fairness and Robustness Scores notebook in the cortex-certifai-examples repo.
Assumptions
We do not attempt to recommend hard thresholds for robustness or fairness. That is, we will not make statements like ”if your robustness score is less than 80, then you should figure out how to build a more robust model”. Instead, we recommend setting thresholds that are acceptable for the use case at hand. This is analogous to the way a data scientist would choose acceptable thresholds for performance metrics. For example, in some use cases, an accuracy of 80% is considered good performance, but in other cases (perhaps in more high stakes/high cost situations) 80% accuracy would be unacceptable.
Certifai’s entire analysis (except for the performance score) is based on the generation of counterfactual explanations for a supplied evaluation dataset and a model. A counterfactual explanation for a given data point is a minimally perturbed version of that data point that receives a different prediction from the model than the original data point.
Introduction
The two plots below show examples of counterfactual explanation points (yellow points) for one input data point (black point) under two different models that have been trained on the same dataset with different parameters. We can see that the counterfactual explanation (yellow point) is close to the original data point (black point) but just over the decision boundary (where the orange and blue regions meet). However, the key thing to notice is that since the boundaries for the models are different, the counterfactual explanations are different distances from the original point.
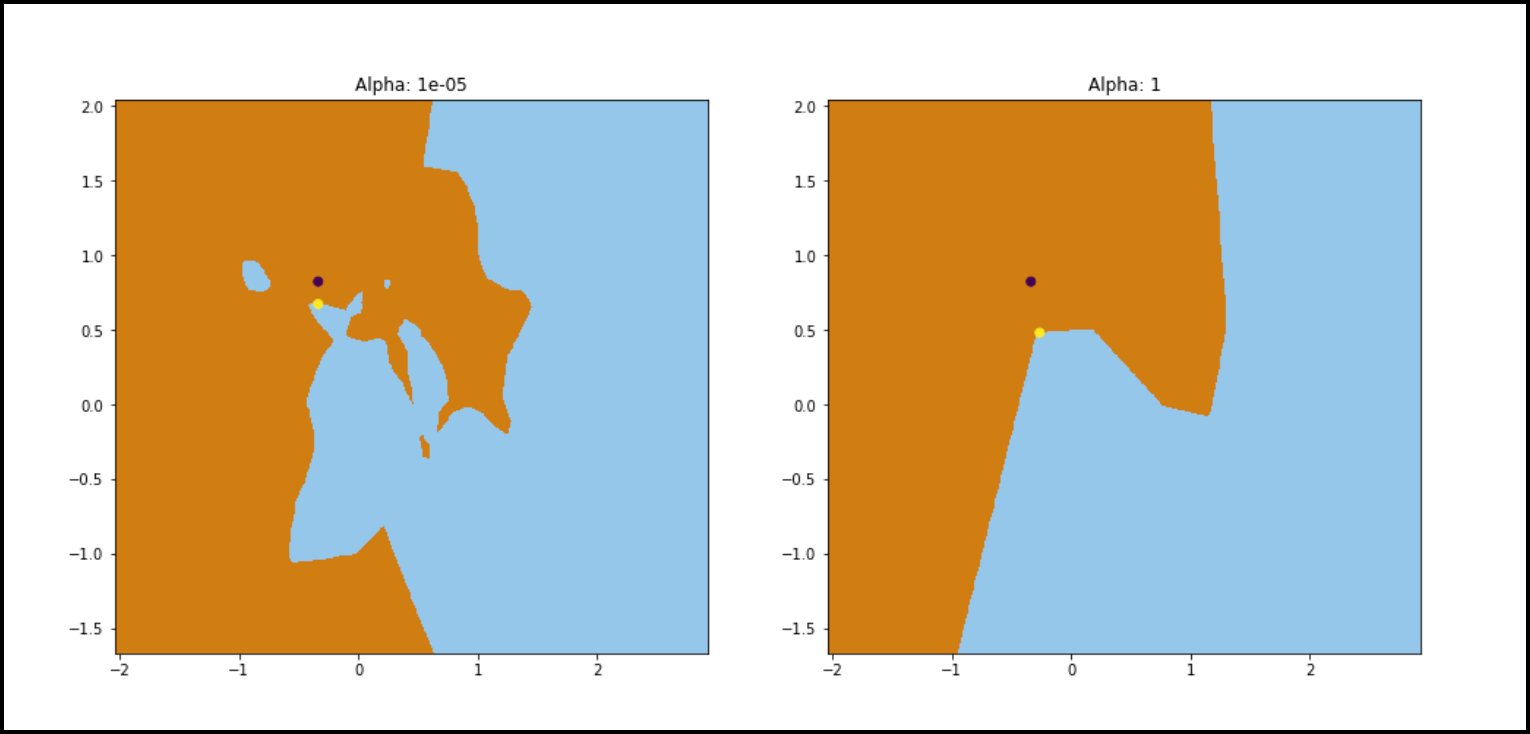
Certifai finds counterfactual explanations for a given model and dataset and then uses characteristics of aggregated counterfactual explanations to calculate the robustness, fairness, and explainability scores. In this document, we will use a simple simulated dataset to train models and show how the robustness score and fairness score generated by Certifai can be used to assess model performance.
Setting Up the Data and Training Candidate Models
To get started, we generate some two-dimensional data using the make_moons function in the sklearn package. We choose two dimensions to make it easy to visualize.
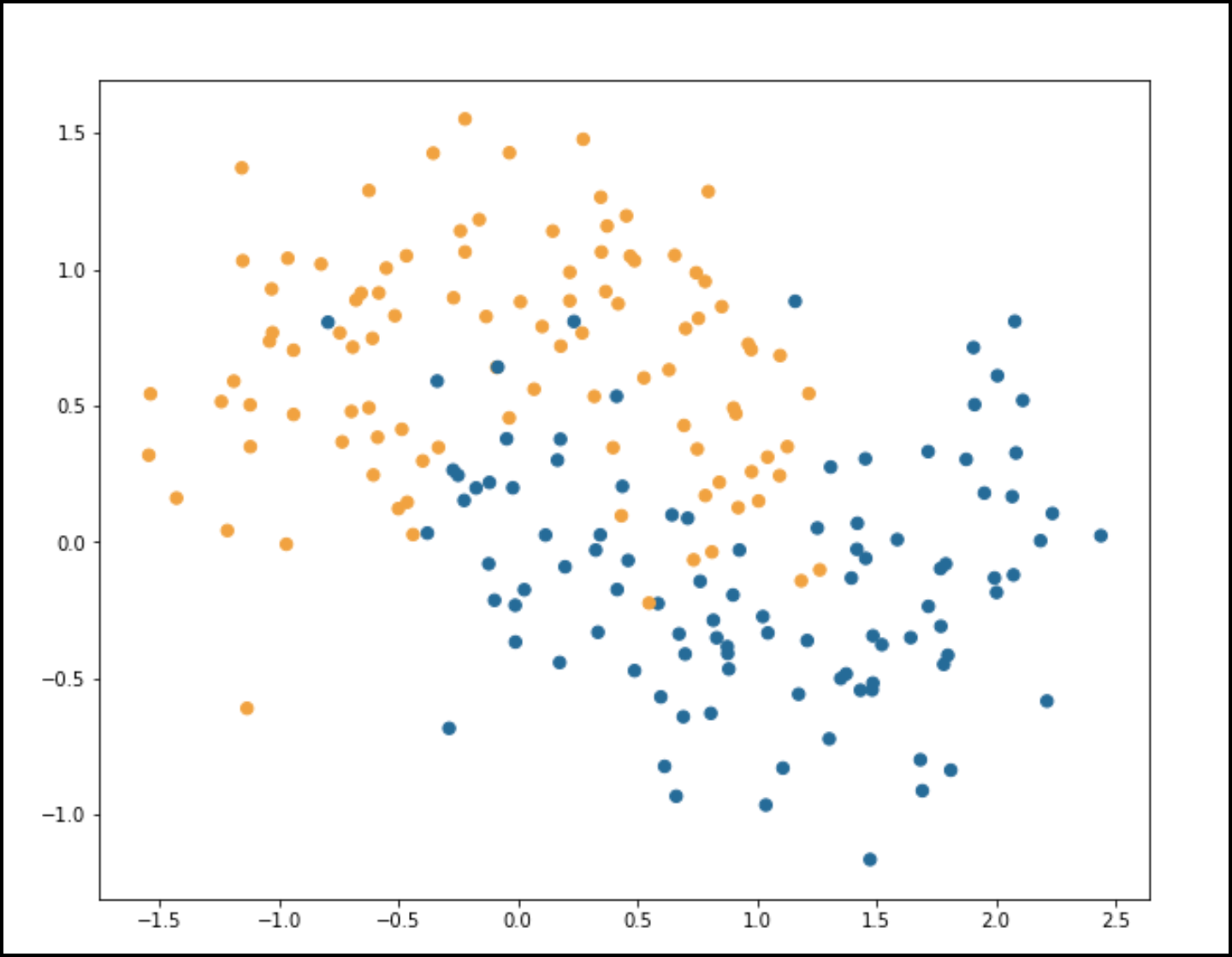
The yellow dots and black dots come from different distributions, and the goal is to train a model that is able to classify the yellow dots as class 0 and the black dots as class 1 as accurately as possible while also balancing concerns like robustness and fairness. We use a Multilayer Perceptron (MLP), which is a simple neural network, to classify these points. As with any modeling problem, we want to maximize performance on the training set but also set the model up to perform well on future, unseen data. That is, we want to avoid overfitting, and so we fit a whole set of models varying parameters, looking for a model that balances these two aims.
In order to change the closeness of the fit to the training data,, we're going to vary the alpha parameter of the MLP. Since our dataset only has two variables, we can quickly assess how complex the model is by plotting the boundary the MLP arrives at for different values of alpha. In the figure below, we’ve drawn in the decision boundary and colored the region with the label that the model gives to points that lie in this region. For example, if a point is in the blue region, the model labels it as a 1. The dots are colored with their actual label, so if a yellow dot is in the blue region (or vice versa) that means the model has misclassified it.
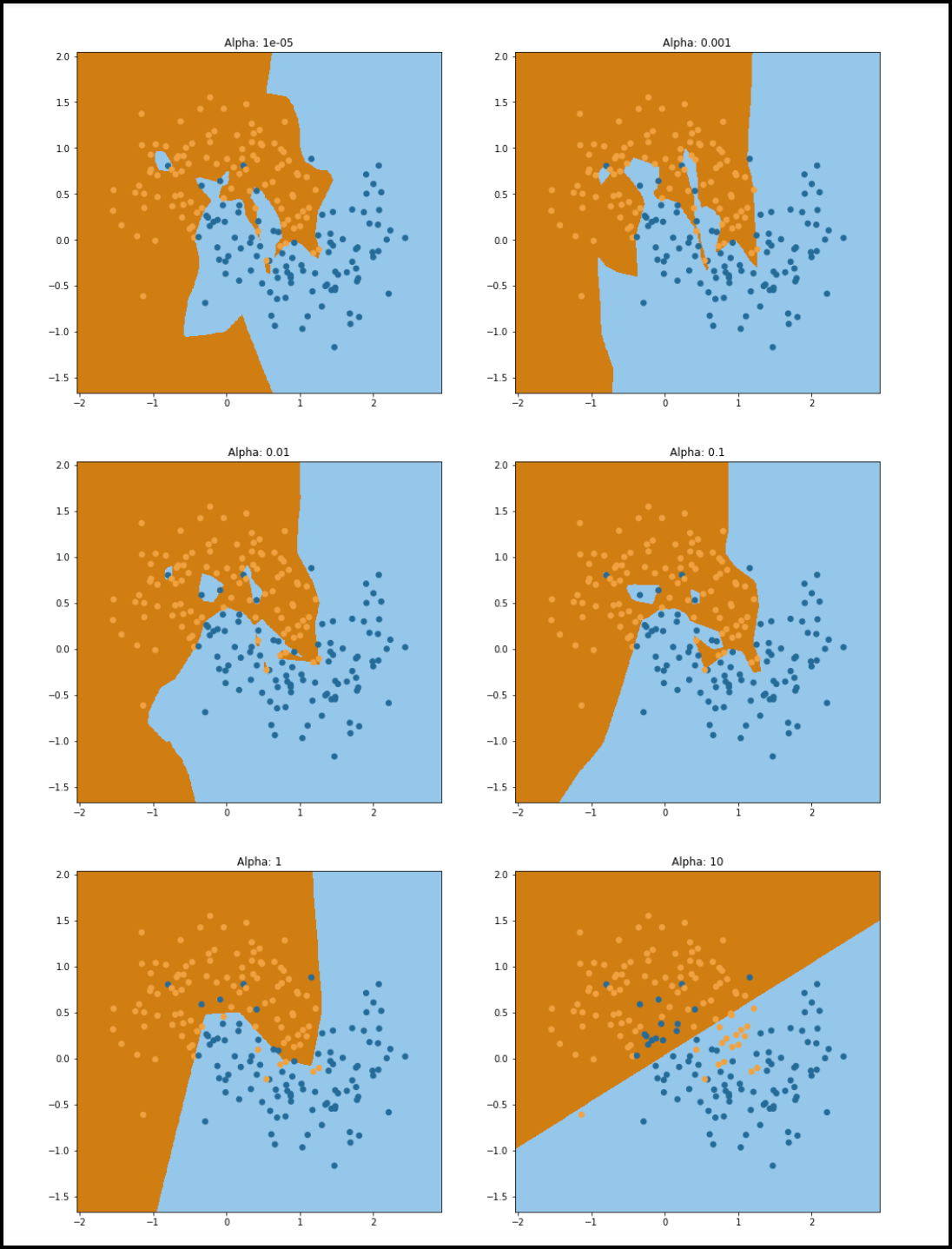
Assessing Fit and Robustness
In the graphs above we see that for smaller values of alpha (e.g., alpha = 1e-5), the boundary is complex and tries to separate as many of the yellow and black points as possible. As alpha increases, the boundary becomes less complex and has a better chance of generalizing to future data. When alpha = 1, the boundary does a good job separating the yellow and black points, but for values larger than 1, the boundary is not complex enough and is probably underfitting the data.
In datasets that involve more than two features, this visual assessment is more difficult or impossible to infer, so we use performance metrics to assess whether or not there is overfitting. We now assess how the model predicts the classes of the training data and on an unseen dataset. Here we can calculate accuracy and Certifai’s robustness measure. At a high level, Certifai’s robustness score measures on average how far all input data points are from their counterfactual explanations. If on average points are very close to their counterfactual explanations (as in the graph of Alpha = 1e-.05), then they are very close to the boundary, which could be a sign of the model fitting the data points too closely (i.e., of overfitting).
| input | alpha | train_robustness | train_accuracy | test_robustness | test_accuracy |
|---|---|---|---|---|---|
| 0 | 0.00001 | 12.17 | 99.5 | 15.06 | 92.0 |
| 1 | 0.00100 | 11.23 | 99.0 | 9.94 | 84.0 |
| 2 | 0.01000 | 13.07 | 99.0 | 12.52 | 90.0 |
| 3 | 0.10000 | 13.23 | 99.5 | 15.62 | 94.0 |
| 4 | 1.00000 | 21.08 | 92.0 | 22.96 | 94.0 |
| 5 | 10.00000 | 53.38 | 83.0 | 53.37 | 86.0 |
The accuracy metrics in the table above reflect what we saw with the boundaries in the graphs. If alpha is small, the accuracy on the training set is high, but the model does not generalize to the test set (i.e., low test accuracy). The models with larger alphas generalize better until you hit a tipping point where the model can no longer capture the complexity of the data, and it performs poorly on both the training and test data (alpha = 10). The robustness scores tell a similar story. The scores are less than .15 where the value of alpha encourages a closer fit to other data (alpha <= .1), and it jumps up to 21.09 when alpha is equal to 1. Based on the high accuracy on the training and test sets and the robustness measure, we would choose alpha to be equal to 1.
So what is the use of the robustness score when you have access to performance metrics? For one, the robustness score will tell you a bit about the complexity of the model’s decision boundary and how the data lies in relation to that boundary, which more traditional performance metrics will not. Furthermore, and perhaps more important, when we are in a production setting, we do not need access to the ground truth to calculate the robustness score. This means we can track performance over time without collecting ground truth labels at every time step. Our recommended use of the robustness score is then:
- Measure metrics (including BOTH robustness and ground-truth-based measures) as we did above when tuning hyper-params.
- Choose the best settings based on the ground-truth-based measures, which is what a data scientist would traditionally do.
- Note the robustness score.
- In production, make sure that the robustness score does not drift too far below (or above) that chosen value.
Fairness
Next, we’ll show how different relationships between the data and the ground truth outcome feature can result in unfair treatment. To do this we use Certifai’s fairness score. The fairness score is useful when some model predictions are considered more favorable than others (e.g., a model is predicting whether a loan should be granted or denied; where obtaining the loan is preferred from the customer’s perspective). When there is a concept of a favorable outcome, we assess whether or not the model is predicting that groups of individuals defined by a protected feature (e.g., gender, age, etc) get the favorable prediction more often than other groups.
Certifai’s fairness monitoring is flexible. It can help you examine fairness issues where:
- A protected feature was used to train a model (i.e., the model could show explicit bias),
- The protected feature was not used during training (i.e., the model could show implicit bias).
Explicit bias occurs when the protected feature is used during training, and it is correlated with the outcome. The model then explicitly uses that feature to make predictions.
Implicit bias occurs when the model was not explicitly trained using the protected feature, but the protected feature could be correlated with other features. Even though the model did not use the protected feature during training, it can leak into the model through the correlated feature.
In a farfetched example, let’s say we build a model that uses height to decide whether to grant a loan, and if you’re taller, you’re more likely to get a loan for some reason. However, height and gender are correlated, so by using height, you’re also implicitly using gender to make the decision.
In both cases, we can tell Certifai to perform fairness analysis for the protected attribute. For the implicit bias case you also have to supply the protected feature. Certifai calculates a measure called burden for each subgroup in the protected feature, and it then uses these burden scores to calculate a single number, which we refer to as the fairness score. The burden is measured by subgroup as the average distance between their original features and the features in their counterfactual explanations for those people who received the unfavorable prediction. For people who received the favorable outcome, this distance is zero: such individuals contribute to the denominator but not the numerator.
In this example, we examine implicit bias for a binary protected attribute in the following situations:
- The protected attribute and the ground truth outcome are identical
- The protected attribute and the ground truth outcome are completely uncorrelated (i.e., the protected attribute value is determined by flipping a fair coin)
- One subgroup within the protected attribute is more likely to have the favorable outcome in the ground truth than the other subgroup
The first two cases are the most extreme examples of bias (1) and fairness (2), and the third example is somewhere in between. For each situation, we use the model trained with alpha = 1 and calculate burden and the fairness score. Note here that we did not use the protected feature during model training.
First, we look at the burden plots in each of the scenarios. The first plot shows where the protected attribute and the ground truth outcome are identical.
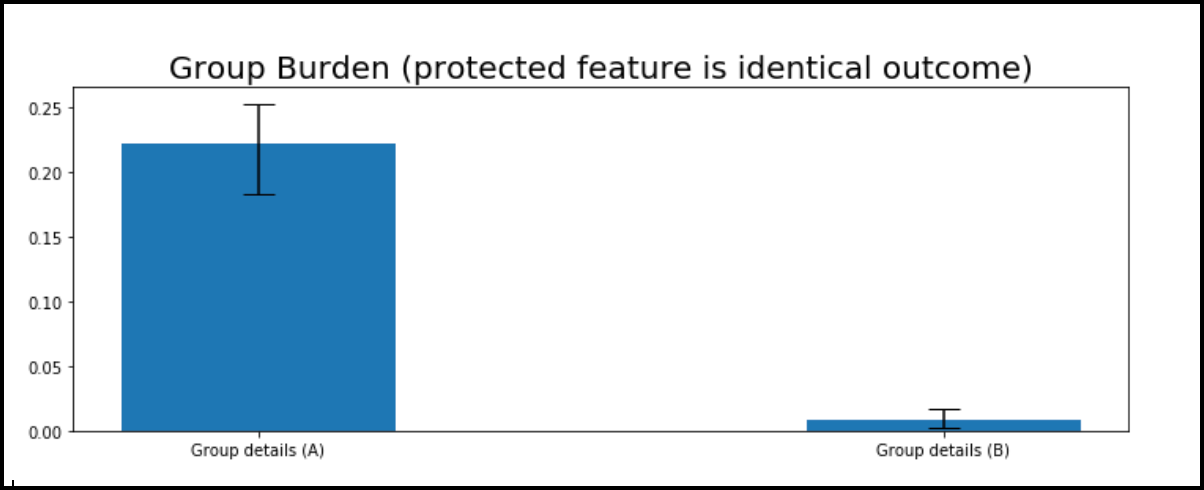
According to the graph above, group A has more difficulty attaining the favorable prediction from the model. Since models learn the boundary that classifies as many things correctly as possible and group A is identical to the group that has the unfavorable outcome in the ground truth, most of group A is given the unfavorable prediction (true negatives). Here, the distance between the original points and their counterfactuals contributes to the burden. On the other side, most people in group B receive the favorable prediction (true positives) and contribute zero to the numerator. A small number of false negatives in group B make the burden greater than zero. This is an extreme example of implicit bias.
In the next scenario, we go to the other extreme and establish no association between the protected feature and the outcome by randomly assigning an A or B to each observation in the dataset. The burden for that case is depicted in the graph below.
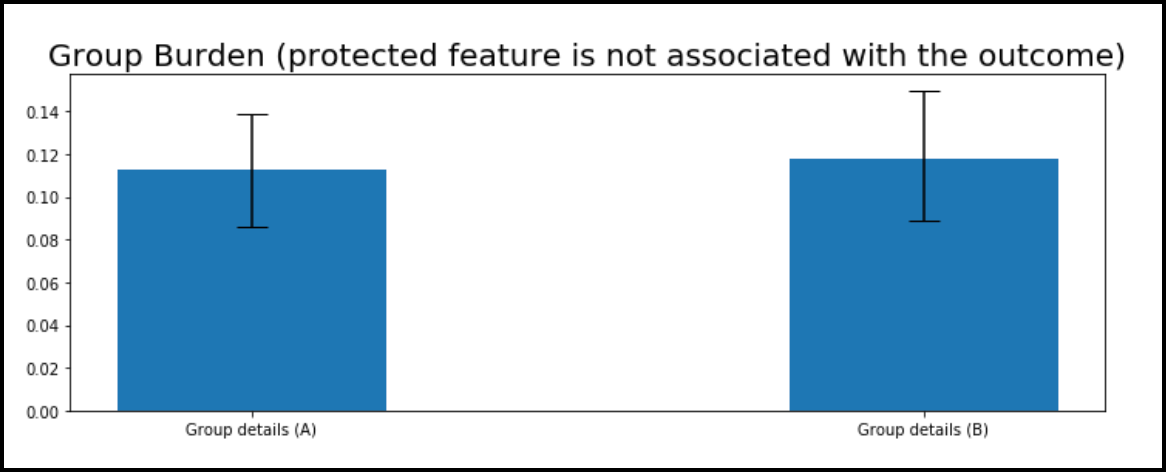
We see in the graph above that the burdens for group A and B are roughly equal (or at least their error bars are overlapping), which means it's not too difficult for either group to obtain the favorable prediction relative to the other group.
However, in most situations the protected feature is not perfectly correlated with the outcome in the ground truth or completely uncorrelated with the outcome. In most cases there is some correlation between the protected feature and the outcome. To mimic this we divide the observations based on the favorable and unfavorable ground truth labels, and within each group, randomly draw the value of the protected feature with different probability. Specifically, we assign observations in the favorable group to be group A with 25%, and in the unfavorable group, we assign observations to be group A with 75% chance. The burden plot for that situation is displayed below.
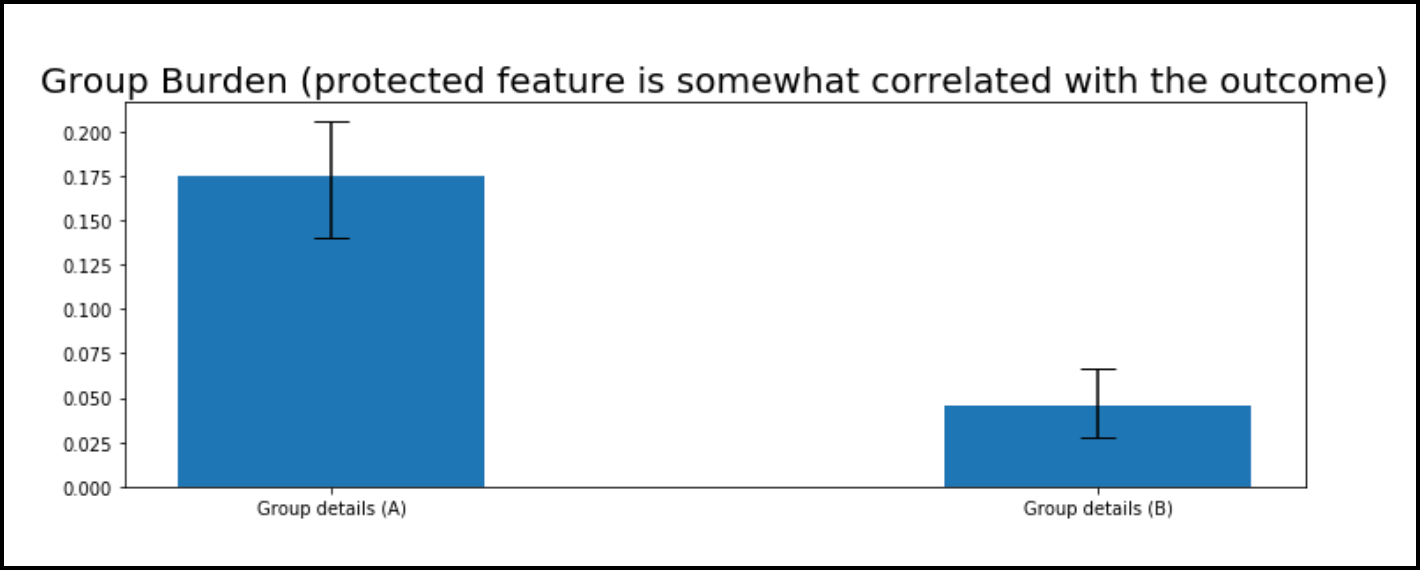
In this situation we can see that there is a difference between the burdens of the two groups with group A having a burden of around .175 and group B having a burden of around .05.
However, comparing these burden plots across models becomes unwieldy, which is why we use the burden values to calculate a normalized fairness score. The fairness score is a gini-like index between 0 and 100 that essentially measures how unequal the burden values are across groups. A score of 0 means the model is exhibiting the highest bias and a score of 100 means the model is perfectly fair.
The table below shows the Fairness score for each scenario above.
| type | overall fairness | overall fairness lower bound | overall fairness upper bound |
|---|---|---|---|
| protected feature determines outcome | 7.169127 | 2.371643 | 13.995314 |
| protected feature not related to outcome | 93.021066 | 80.419179 | 99.398914 |
| protected feature partially relates to outcome | 41.789661 | 27.018751 | 56.131344 |
Having seen the burden plots, the overall fairness scores match up with our expectations. In the case where the protected feature is identical to the ground truth outcome, the number is close to zero. When there is some association between the protected attribute and the ground truth outcome then the fairness score is around 42, and when there is no association between the protected attribute and the ground truth label, the score is around 93.
This example illustrates how relationships between the data and the outcome can result in the different treatment of subgroups within a protected feature.
Conclusion
We’ve shown how the robustness and fairness scores can vary under different conditions and what they can tell you about the robustness or fairness of your models. We’ve also shown that Certifai is flexible; it does not require ground truth to give you a performance metric like robustness, and it can measure both implicit and explicit bias.
It’s important to note that there aren’t hard thresholds for which a model is not robust or a model is not fair. This will depend on the specific modeling scenario. In general, as data scientists, we do not expect hard thresholds in other performance metrics but aim to surpass performance metrics relative to the problem at hand. Certifai allows us to examine a model’s performance through several different lenses in order to understand it and track its performance through time.
 Cortex Certifai
Cortex Certifai